
(C)インターネットランド>中学校>3年生>数学>発展問題>プラトーの問題
正方形の4つの頂点を結ぶ最短の線を求める問題。枠に張られた石鹸膜から実験的に解決された。『TOSS授業ライセンスセミナーin関西』(2005.5.28)でC表で12級。TOSS九州ライセンスセミナー(2006.2.5)で4級に認定された授業です。
1.プラトーの問題とは
プラトーの問題とは、『空間に1つの閉曲線γ(ガンマ)が与えられた場合、その閉曲線を境界にもち、しかもその閉曲面が最少となる曲面を求めよ』という類の問題である。
この問題は実験的に解くことができる。まず、空間内に与えられた閉曲線γを針金で作る。次に、これを石鹸水の中につけてそーっと取り出せば、閉曲線を縁とした石鹸膜が得られるが、この膜は表面張力によってその表面積が最少になるように張られている。したがってこの膜が張る曲面が、求める曲面であるということになる。
この実験は、ベルギーの実験物理学者J.A.プラトー(J.A.Plateau 1801-1883)によって最初に行われたので、この種の実験はプラトーの問題と呼ばれている。
さらに、アメリカの数学者J.ダグラス(Jesse Douglas 1897-1965)は、第1回のフィールズ賞を、プラトー問題の研究によって受賞している。
数学の難問を解く鍵がシャボン玉にあったということは、中学生に科学や数学への興味・関心を向けさせることができる。解が分かれば、三平方の定理や直角三角形の辺の比を使って経路の長さの計算ができることから、中学校数学の最後の単元に位置づけて扱う。
2.授業の流れ
シャボン玉を作って見せる。
発問1 シャボン玉です。どんな形をしていますか。
(球)
発問2 なぜ、球になるのですか。
(表面張力がはたらくから)
説明1 表面張力がはたらき、表面積が最小になろうとするのです。
発問3 立方体のシャボン玉はできるでしょうか。できると思う人?できないと思う人?
立方体のシャボン玉の画像を見せる。 
説明2 立方体の枠を石けん液につけます。2回つけたとき、中に立方体のシャボン玉ができています。
このように 枠に張られた石鹸膜に関する問題をプラトーの問題といいます。
指示1 プラトーの問題に挑戦してみましょう。
問題1 1辺10kmの正方形の頂点にA,B,C,Dの4つの島があります。これらの島を海底トンネルで結びます。 どのように結べば、最短の経路になりますか。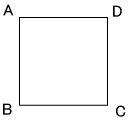
指示2 考えられる経路をノートにかきなさい。1つかけたら持ってきなさい。
速く書けた人に、板書してもらう。
指示3 かけた人は長さがいくらになるか計算しなさい。ただし、√2=1.4、√3=1.7とします。
説明3 ここで、立方体に張った石鹸膜を思い出してください。ある方向から見ると石鹸膜によって、A,B,C,Dが
結ばれます。これが4つの点を結ぶ最短経路となるのです。 
解 交点をX,Yとし、AD平行BC平行XYとする。∠AXB=∠DYC=120°とする。
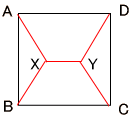
説明4 アメリカの数学者ダグラスはこのプラトーの問題を研究して数学で最も名誉な賞であるフィールズ賞を受賞しました。
発問4 経路をつなぎ合わせていきます。どんな形になりますか。
(六角形)
発問5 さらにつなぎ合わせます。何を連想しますか。
(蜂の巣)
説明5 蜂は最小の面積・最少の材料で巣を作る方法を本能で知っているのです。また、魚の縄張りもこの形になっています。
説明6 自然の中に存在していた真理は、20世紀になり、数学の偉大な発見として、私たちに知られるようになったのです。
説明7 そのきっかけは、私たちが幼いころ遊んだシャボン玉でした。身の回りのことを、科学の目で見つめ直してみると、すばらしい発見があるかもしれませんね。
3.参考文献
「おかしなおかしな数学者たち」 矢野健太郎/新潮文庫
「かたち探検隊」 小川泰/岩波科学ライブラリー
「プラトーの問題」